The spiral is a popular pattern for those who like to draw and design and it is also one of nature’s most common configurations. In fact, it’s difficult to think of all the things that have a spiral pattern. Snail shells, flower petals, pine cones, snakes, storms, DNA, curly hair, even galaxies are spirals—and that’s not even nearly all!
Why are spirals so abundant in nature? No one can say for certain, but a possible answer is, because spirals are the smart way to grow!
The Golden Ratio:
The Golden Ratio refers to a simple equation that translates to mean, “two quantities are in the golden ratio if the ratio between them is the same as the ratio of their sum to the larger of the two quantities" or a/b = (a+b)/a.
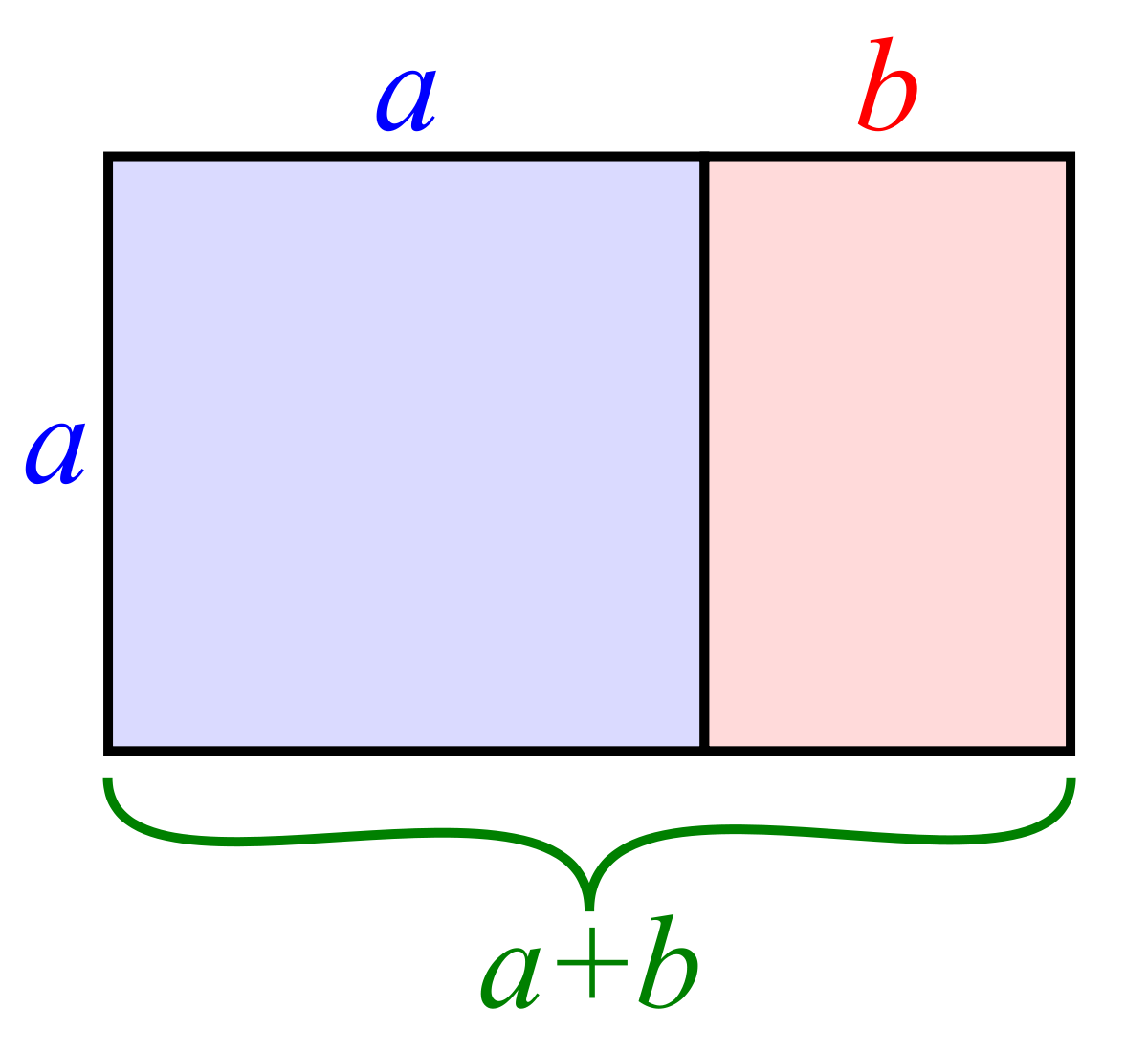
In visual art like painting and photography, the golden ratio is used in composition because it is considered aesthetically pleasing.
The Fibonacci Spiral
In nature, the golden ratio can be observed in how things grow or form.
This can best be explained by looking at the Fibonacci sequence, which is a number pattern that you can create by beginning with 1,1 then each new number in the sequence forms by adding the two previous numbers together, which results in a sequence of numbers like this: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 and on and on, forever.
The further along the Fibonacci sequence you go, the closer the ratio between successive numbers in the sequence gets to Phi, or 1.618, which is the Golden Ratio.
To see a Fibonacci spiral, draw a series of squares with sides the length of the numbers in the sequence: a 1x1 square, a 2x2 square, a 3x3 square, 5x5 and so on until you get something that looks like this:
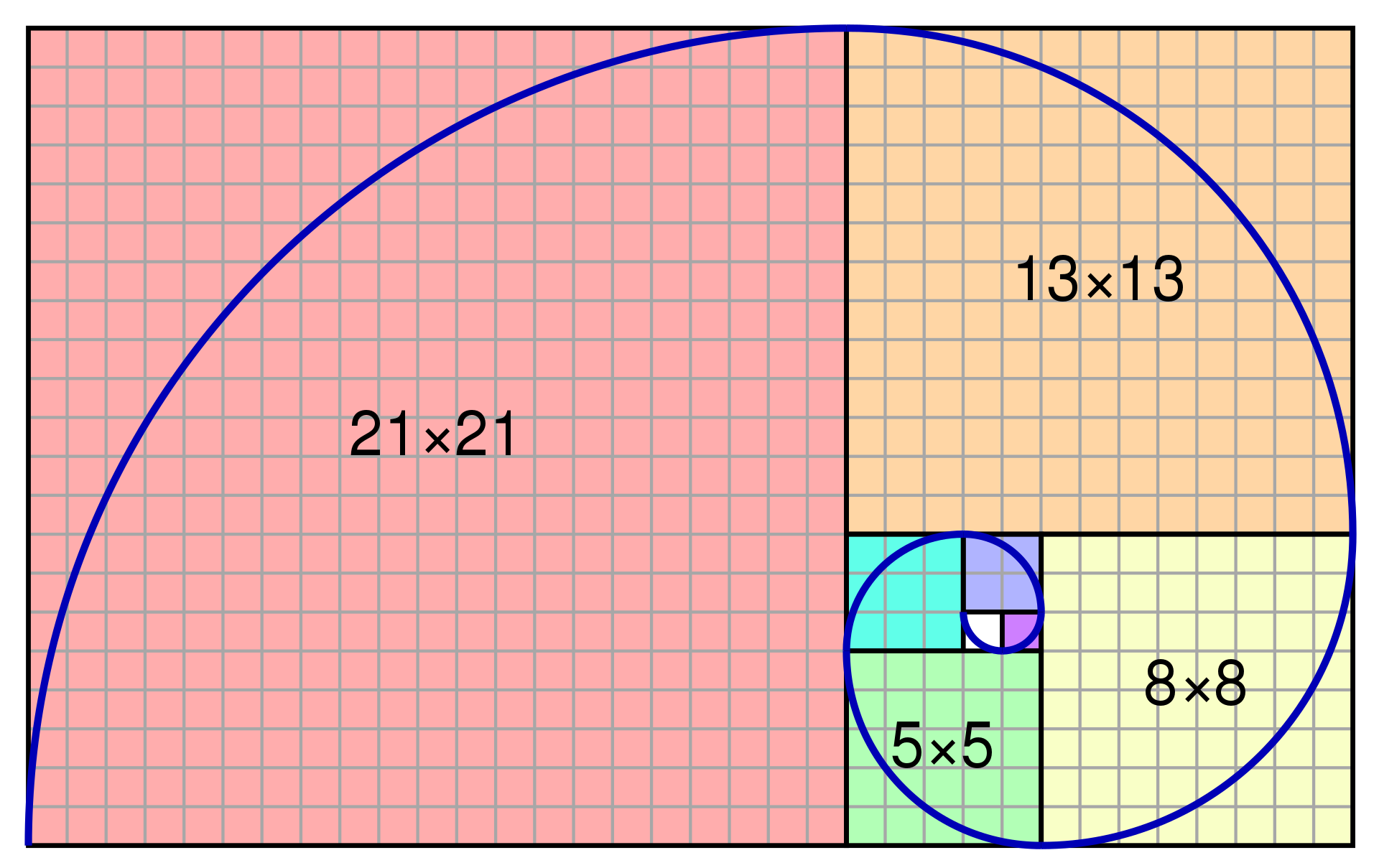
Once you have your squares, you can use them to trace a perfect spiral by drawing a curve from corner to corner.
When this is applied to nature, say something like a flower, each petal would develop a factor of the Golden Ratio away from the last petal, allowing a spiral to form.
While we can’t be entirely sure why something grows in a spiral, it could be a matter of efficiency. A spiral is an excellent way to maximize space! If you consider the arrangement of seeds on a sunflower, the spiral is the best way to house the most seeds on the face of the flower. The more seeds you are able to house, the more future sunflowers are possible.
You will also find that the leaves on the stalk follow a spiral pattern, this could be to maximize the amount of sun they can collect by spreading themselves strategically around the stalk. Who knew flowers were so smart?
How to Spot Fibonacci Spirals
You can actually see the Fibonacci sequence in action in some natural spirals. Take this pinecone for instance. Count the spirals going in one direction.

Now, try counting the spirals going in the other direction.
What numbers did you get? We counted 8 going one way and 13 going the other way. The numbers 8 and 13 are both Fibonacci numbers!
You can even do this with a sunflower, although it will take longer. Do you still come up with a Fibonacci number?

We counted 21 and 34, which are Fibonacci numbers. Did you count the same? This doesn’t happen all the time, but frequently you will find Fibonacci numbers occurring in nature. What are some interesting places that you’ve observed spirals in nature, or even in art and architecture?
Learn something new?
If you learned something from this post and you want to help us keep science resources and programs free for kids accross the province, consider making a donation to support Science World's mission.