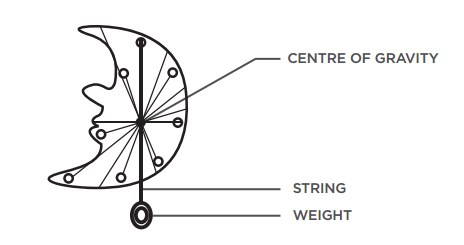
Finding the centre of gravity of an irregularly-shaped object is trickier than for a ruler or other regular shape. In this activity, students use the force of gravity to deduce the centre of gravity for various shapes.
Since the weight of an object is concentrated in its centre of gravity, the force of gravity passes through this point in a vertical line towards the Earth. An object hanging from any point will automatically rotate so that its centre of gravity is along this vertical line from the hanging point.
In this activity, a plumb line (a weighted string) is created in order to visualize the vertical gravitational pull towards the Earth. Hanging the shape at any point will cause the shape to rotate until its centre of gravity lines up directly below the hanging point.
Drawing a line along the plumb line enables us to see the vertical line between the hanging point and the centre of the earth. The problem is that one line is not sufficient to pinpoint the exact centre of gravity of the shape (it could be anywhere along this line). This is why we hang the shape at a different point and draw another line along the plumb line.
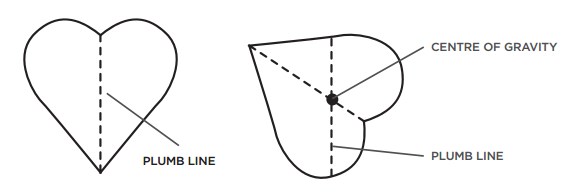
The intersection of the two plumb lines is the object's centre of gravity. When students hang the shape from several different points they see that the plumb line always passes through the same spot.
You have correctly marked the shape's centre of gravity if:
- when you pin your shape through its centre of gravity it is stable and balanced.
- you can balance the shape by placing your finger under the centre of gravity.
An object will topple over once its centre of gravity falls outside its base of support. To answer a brainteaser on whether or not an object will topple over, students can draw a plumb line between the object's centre of gravity and its base. If the plumb line falls outside of the base of support, the object will topple over. This is why the Leaning Tower of Pisa does not topple over: its centre of gravity is still above its base when a plumb line is drawn. If it were leaning more, it would topple over since the plumb line would fall outside the base.