This game recreates Archimedes' "Eureka!" moment, without having to take a bath. Students participate in a relay race that tests their speed and skill in measuring the water displaced by an egg.
The Story:
Archimedes was asked by a king to figure out whether the king's crown was pure gold or gold mixed with silver. Archimedes knew that he had to figure out the crown's density: how heavy it is compared to how much space it takes up (which is mass divided by its volume). It was easy enough to figure out how heavy it was but its volume was tricky.
Archimedes went off to think about this in a nice hot bath. While he was in the bath he noticed that the more of himself he put under water, the higher the water level rose. He realized that the amount of water that rose was equal to his own volume. He was (supposedly) so happy to make this discovery that he ran out into the streets naked shouting "I found it!" ("Eureka!").
Archimedes had found an easy way to measure the volume of an irregularly shaped object. If you submerge the object in water, it will displace a volume of water equal to its own volume. He could use this method to find the volume, and thus the density of the crown. Legend has it that he was able to compare the crown's density to the density of gold, and thus show that the metal in the crown wasn't pure.
Our Eggsperiment:
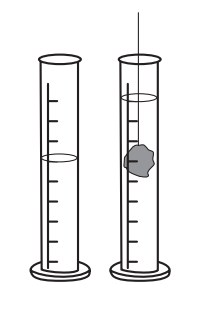
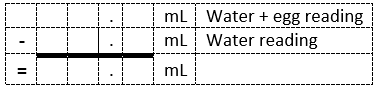
When we fill up a glass with water, put an egg in the glass and measure the water that rises up (or spills out), we discover the volume of the egg.
Here's an example of the method used in this activity:
Imagine 20.0 ml of water in a cylinder. Put an object into the water you will see how the level of water in the cylinder has moved up (to 23.0 ml, for example). The volume of displacement is how much the water level has changed (in this case, it is 3.0 ml). The volume of the object is equal to this amount because it is the amount of space that it took up while in the water. In other words, the volume of the displaced water is equal to the volume of the object.